Stochastic Approximation fitting of MRFs on 2d lattices

Estimates the parameters of a MRF by successively sampling from a parameter configuration and updating it by comparing the sufficient statistics of the sampled field and the observed field.

This method aims to find the parameter value where the gradient of the likelihood function is equal to zero.

fit_sa(
  Z,
  mrfi,
  family = "onepar",
  gamma_seq,
  init = 0,
  cycles = 5,
  refresh_each = length(gamma_seq) + 1,
  refresh_cycles = 60,
  verbose = interactive()
)

Arguments

Z

A matrix object containing the observed MRF. NA values can be used to create a subregion of the lattice for non-rectangular data.

mrfi

A mrfi object representing the interaction structure.

family

The family of parameter restrictions to potentials. Families are: 'onepar', 'oneeach', 'absdif', 'dif' or 'free'. See mrf2d-familiy.

gamma_seq

A numeric vector with the sequence of constants used in each step $\gamma_t$.

init

The initial value to be used in the optimization. It can be:

A valid array of parameter values according to family.
0. If set to 0 an array with `0`` in all entries is created.

cycles

The number of updates to be done (for each each pixel).

refresh_each

An integer with the number of iterations taken before a complete refresh (restart from a random state). This prevents the sample from being stuck in a mode for too long. Defaults to length(gamma_seq) + 1 (no refresh happens).

refresh_cycles

An integer indicating how many Gibbs Sampler cycles are performed when a refresh happens. Larger is usually better, but slower.

verbose

logical indicating whether the iteration number is printed during execution.

Value

A mrfout object with the following elements:

theta: The estimated array of potentials.
mrfi: The interaction structure considered.
family: The parameter restriction family considered.
method: The estimation method ("Stochastic Approximation").
metrics: A data.frame containing the the euclidean distance between the sufficient statics computed for Z and the current sample.

Details

The stochastic approximation method consists of, given an observed field Z, and a starting parameters configuration $\theta_0$, successively sample a field $Z_t$ from the current parameter configuration and estimate the direction of the gradient of the likelihood function by comparing the sufficient statistics in the current sample and the observed field.

The solution is updated by moving in the estimated direction with a predefined step size $\gamma_t$, a new field $Z_{t+1}$ is sampled using the new parameter configuration and $Z_t$ as an initial value, and the process is repeated.

$$\theta_{t+1} = \theta_t - \gamma_t(T(Z_t) - T(Z)),$$ where $T(Z)$ is the sufficient statistics for the reference field, $T(Z_t)$ is the sufficient statistics for a field sampled from $\theta_t$.

gamma_seq is normalized internally by diving values by length(Z), so the choice of the sequence is invariant to the lattice dimensions. Typically, a sequence like seq(from = 1, to = 0, length.out = 1000) should be used for defining a sequence with 1000 steps. Some tuning of this sequence is required.

Note

Stochastic Approximation is called "Controllable Simulated Annealing" in some references.

Examples where Stochastic Approximation is used with MRFs are (Gimel'farb 1996) , (Atchadé et al. 2013) .

References

Wikipedia (2019). “Stochastic approximation.” https://en.wikipedia.org/wiki/Stochastic_approximation.

Atchadé YF, Lartillot N, Robert C, others (2013). “Bayesian computation for statistical models with intractable normalizing constants.” Brazilian Journal of Probability and Statistics, 27(4), 416--436.

Gimel'farb GL (1996). “Texture modeling by multiple pairwise pixel interactions.” IEEE Transactions on pattern analysis and machine intelligence, 18(11), 1110--1114.

Author

Victor Freguglia

Examples

# \donttest{
set.seed(2)
fit1 <- fit_sa(Z_potts, mrfi(1), family = "oneeach", gamma_seq = seq(1, 0, length.out = 50))
#> 
 Iteration: 1
 Iteration: 2
 Iteration: 3
 Iteration: 4
 Iteration: 5
 Iteration: 6
 Iteration: 7
 Iteration: 8
 Iteration: 9
 Iteration: 10
 Iteration: 11
 Iteration: 12
 Iteration: 13
 Iteration: 14
 Iteration: 15
 Iteration: 16
 Iteration: 17
 Iteration: 18
 Iteration: 19
 Iteration: 20
 Iteration: 21
 Iteration: 22
 Iteration: 23
 Iteration: 24
 Iteration: 25
 Iteration: 26
 Iteration: 27
 Iteration: 28
 Iteration: 29
 Iteration: 30
 Iteration: 31
 Iteration: 32
 Iteration: 33
 Iteration: 34
 Iteration: 35
 Iteration: 36
 Iteration: 37
 Iteration: 38
 Iteration: 39
 Iteration: 40
 Iteration: 41
 Iteration: 42
 Iteration: 43
 Iteration: 44
 Iteration: 45
 Iteration: 46
 Iteration: 47
 Iteration: 48
 Iteration: 49
 Iteration: 50
# Estimated parameters
fit1$theta
#> , , (1,0)
#> 
#>            0          1          2
#> 0  0.0000000 -0.9719982 -0.9719982
#> 1 -0.9719982  0.0000000 -0.9719982
#> 2 -0.9719982 -0.9719982  0.0000000
#> 
#> , , (0,1)
#> 
#>           0         1         2
#> 0  0.000000 -1.009834 -1.009834
#> 1 -1.009834  0.000000 -1.009834
#> 2 -1.009834 -1.009834  0.000000
#> 
# A visualization of estimated gradient norm over iterations.
plot(fit1$metrics, type = "l")


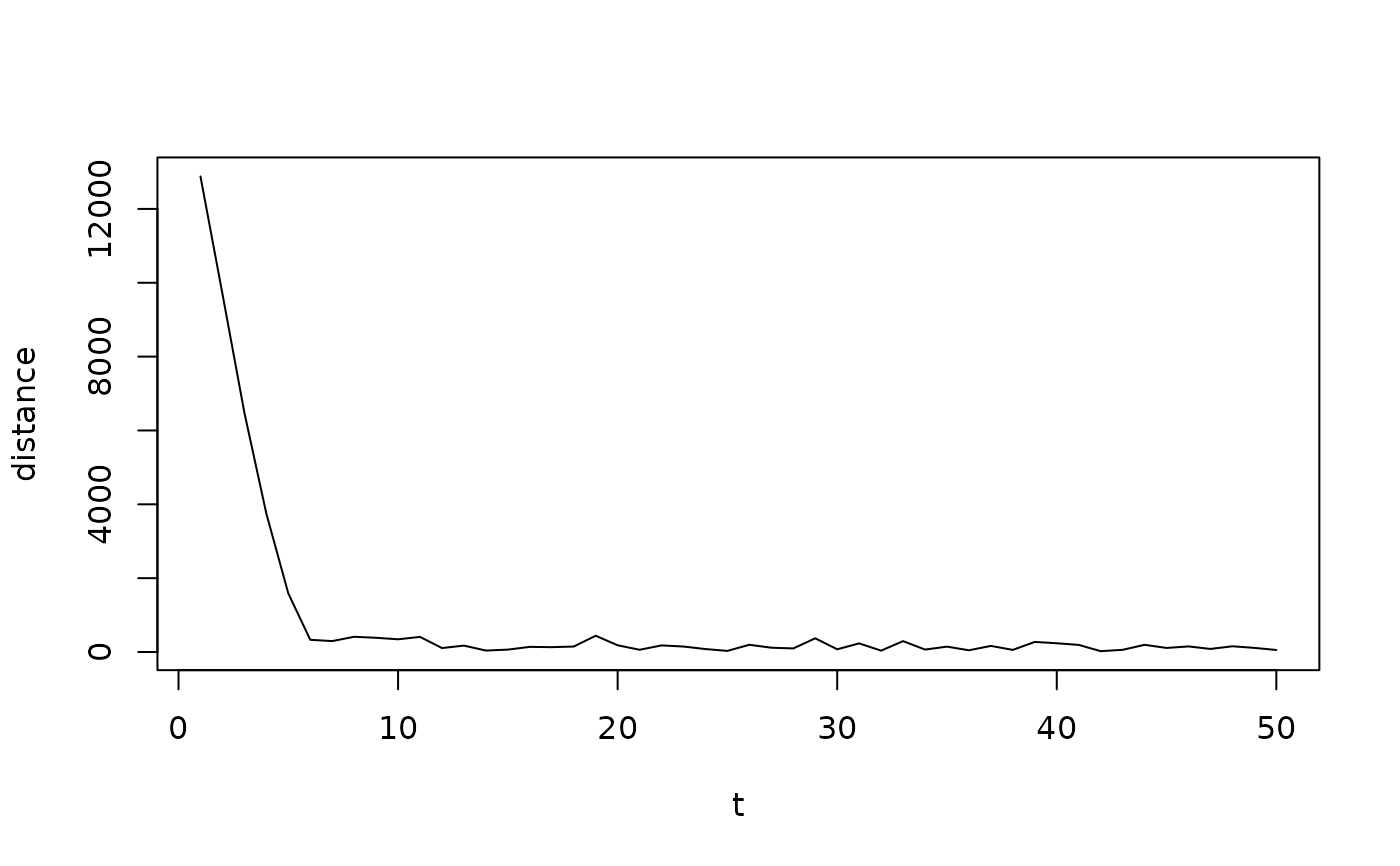fit_sa(Z_potts, mrfi(1), family = "oneeach", gamma_seq = seq(1, 0, length.out = 50))
#> 
 Iteration: 1
 Iteration: 2
 Iteration: 3
 Iteration: 4
 Iteration: 5
 Iteration: 6
 Iteration: 7
 Iteration: 8
 Iteration: 9
 Iteration: 10
 Iteration: 11
 Iteration: 12
 Iteration: 13
 Iteration: 14
 Iteration: 15
 Iteration: 16
 Iteration: 17
 Iteration: 18
 Iteration: 19
 Iteration: 20
 Iteration: 21
 Iteration: 22
 Iteration: 23
 Iteration: 24
 Iteration: 25
 Iteration: 26
 Iteration: 27
 Iteration: 28
 Iteration: 29
 Iteration: 30
 Iteration: 31
 Iteration: 32
 Iteration: 33
 Iteration: 34
 Iteration: 35
 Iteration: 36
 Iteration: 37
 Iteration: 38
 Iteration: 39
 Iteration: 40
 Iteration: 41
 Iteration: 42
 Iteration: 43
 Iteration: 44
 Iteration: 45
 Iteration: 46
 Iteration: 47
 Iteration: 48
 Iteration: 49
 Iteration: 50
#> Model fitted via Stochastic Approximation 
#> 2 interacting positions: (1,0) (0,1) 
#> family: oneeach 
# }